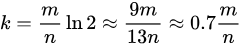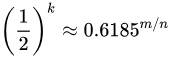最近、AWS Glueのことについて調べていると、Bloom filterがよく出てきました。 Bloom filterは、データの存在確認を効率的に行うための確率的データ構造ですが、wikipediaを見ると偽陽性の発生確率を最小にするパラメータの組み合わせが載っていました。
今日は暇なので、このパラメータが本当なのか/どんな分布なのか簡単にRustで検証してみます。
偽陽性の発生確率を最小にするパラメータ
wikipediaには以下のように記載がありました。
明らかに、m(配列のビット数)が大きければ偽陽性の発生率は低くなり、n(追加する要素数)が多くなれば偽陽性の発生率は高くなる。いま m と n が決まっているとき、偽陽性発生率を最小にする k(ハッシュ関数の個数)は次のようになる。
このときの偽陽性の発生確率は次の通り。
nを固定にし、mとkを変化させた場合、実際に偽陽性がどのように推移するかを検証したいと思います。
- rustのbloomクレートを使います。
- nの値は7000で固定させます。
- mの値は30000から100000まで、kの値は1から7まで変化させます。
use bloom::{BloomFilter};
use rand::{distr::{Alphanumeric, SampleString}, rng};
fn main() {
for m_num_bits in (3*10000..=10*10000).step_by(10000) {
for k_num_hashes in 1..=7 {
calculate_probability(m_num_bits, k_num_hashes);
}
}
}
fn calculate_probability(m_num_bits: usize, k_num_hashes: u32) -> () {
let n = 7000;
let mut filter = BloomFilter::with_size(m_num_bits, k_num_hashes);
create_batch_random_string(n)
.iter()
.for_each(|id| {
filter.insert(id);
});
let validation_count = 100*10000;
let mut hit_count = 0;
create_batch_random_string(validation_count).iter()
.for_each(|id| {
if filter.contains(id) {
hit_count += 1;
}
});
println!("[Input] m_num_bits: {}, k_num_hashes: {}",m_num_bits, k_num_hashes);
println!("[Output] hit_count: {}, probability: {}", hit_count, hit_count as f32/validation_count as f32);
}
fn create_batch_random_string(num: i32)-> Vec<String> {
let mut rng = rng();
let mut strings = Vec::new();
for _ in 0..num {
let random_code = Alphanumeric.sample_string(&mut rng, 40);
strings.push(random_code);
}
strings
}
結果
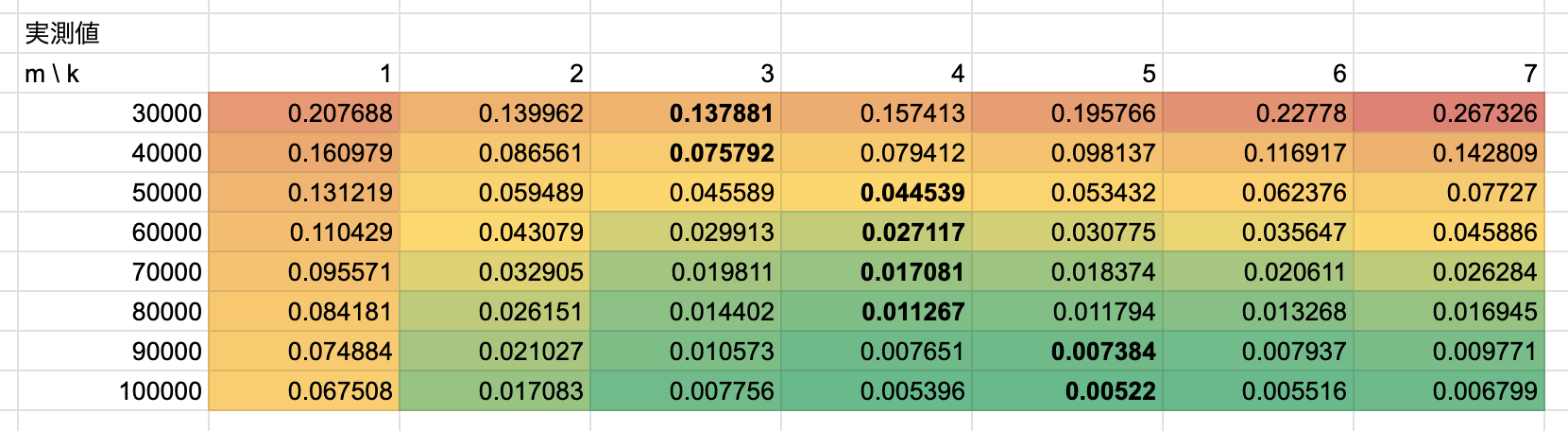
表にまとめてみたのがこちらです↓
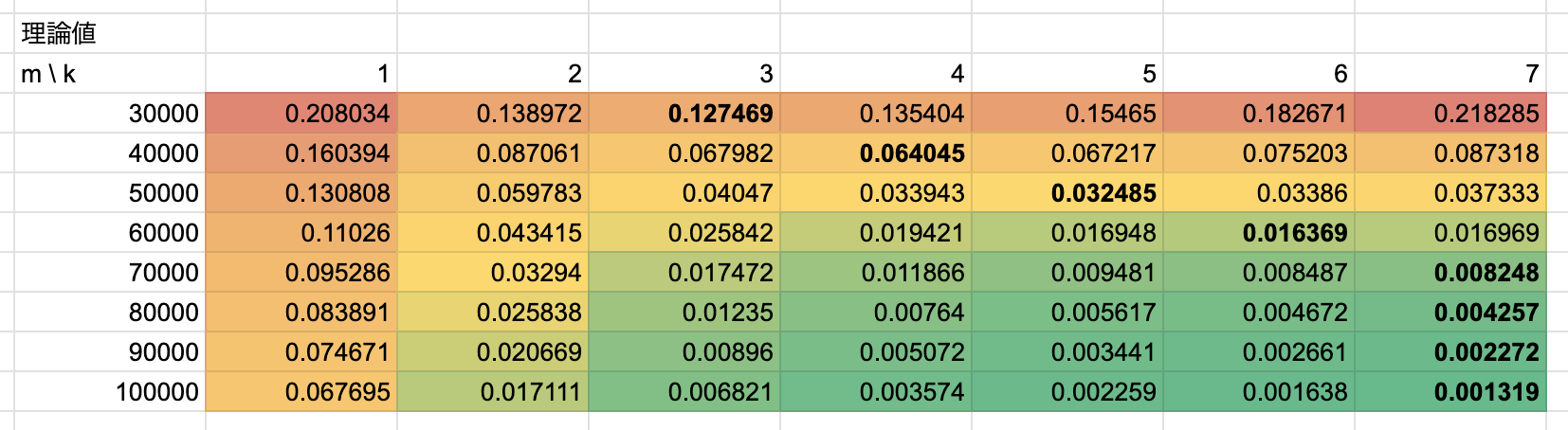
また、念の為理論値も計算してみました↓
- wikipediaに記載の通り、mが増大するにつれて偽陽性の発生確率は低下していきます。
- 最も偽陽性の発生確率が小さいkの値は、mが増大するにつれて増加していきます。
- mが40000以上の場合、理論値と実測値の間でkの値が乖離していることがわかります。
- 原因は謎です🥺… 利用しているライブラリの問題や実行条件が悪かったのかもしれません
- mが40000以上の場合、理論値と実測値の間でkの値が乖離していることがわかります。
参考資料
https://github.com/diggymo/bloom-filter-survey